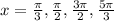Answer:
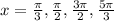
Explanations:
A solution lies where two functions intersect. Given the following functions:
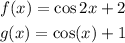
The function intersects at the point where f(x) = g(x) that is:
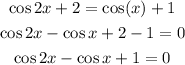
Recall from trigonometry identity that:
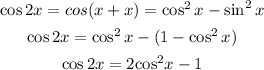
Substitute the expression for cos2x into the quadratic function to have:
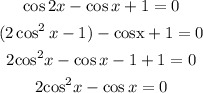
Simplify the result for the value(s) of "x"
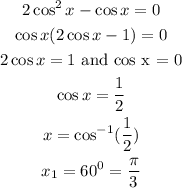
Since cosine is positive in the first and fourth quadrant, the other angles will be:
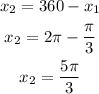
For cos x = 0;
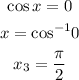
Since cos is also positive in the fourth quadrant, hence;
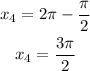
Therefore the values in the interval [0, 2π) that will make the functions
f (x) = cos 2x + 2 and g(x) = cos x + 1 intersect are: