ANSWER
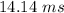
Step-by-step explanation
We want to find the speed of the rock when it reaches the bottom.
The gravitational potential energy of the rock at the top of the hill is equal to the kinetic energy of the rock when it reaches the bottom of the hill. This implies that:
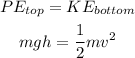
where m = mass of the rock
g = acceleration due to gravity
h = height of the hill
v = speed of the rock at the bottom of the hill
Substituting the given values and solving for v:
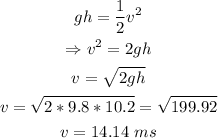
That is the speed of the rock as it reaches the bottom of the hill.