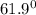Answer:
The expression for the angle is;
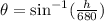
The value of the angle is;
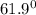
Step-by-step explanation:
Given the figure in the attached image.
The length of the rope is = 680 ft
a)
Using trigonometry;
Recall that;
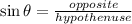
From the diagram;

Substituting we have;
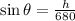
Taking the sine inverse of both sides we have;
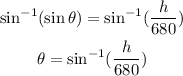
Therefore, the expression for the angle is;
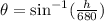
b)
Given that;
The balloon is 600 ft high
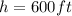
Substituting the value of h into the expression derived in question a;
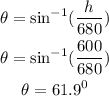
Therefore, the value of the angle is;