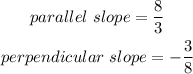Question

Considered the line 8x-3y=2 what slope is parallel to this line and what slope is perpendicular to this line

Answer 1

GIVEN

The equation of the line is given to be:

`8x-3y=2`

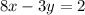
SOLUTION

The equation can be written in the slope-intercept form of a line:

`\begin{gathered} y=mx+b \\ where \\ m=slope \end{gathered}`

This is done by making y the subject of the formula. This is shown below:

`\begin{gathered} \mathrm{Subtract\:}8x\mathrm{\:from\:both\:sides} \\ -3y=-8x+2 \\ \mathrm{Divide\:both\:sides\:by\:}-3 \\ y=(8)/(3)x-(2)/(3) \end{gathered}`

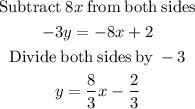
Therefore, the slope is 8/3.

Recall that for parallel lines, the two slopes are equal, and for perpendicular lines, the product of the slopes is equal to -1.

Hence, the parallel slope will be:

`parallel\text{ }slope=(8)/(3)`

and the perpendicular slope can be calculated as;

`\begin{gathered} m_1\cdot m_2=-1 \\ m_1=(8)/(3) \\ \therefore \\ m_2=-(1)/(m_1) \\ m_2=-(1)/((8)/(3)) \\ m_2=-(3)/(8) \end{gathered}`

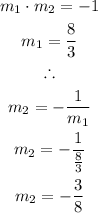
ANSWER

`\begin{gathered} parallel\text{ }slope=(8)/(3) \\ perpendicular\text{ }slope=-(3)/(8) \end{gathered}`