We are given the equations for the elevation of three balloons. These are the following:
For balloon A, we have the graph of a linear equation that passes through the origin, therefore, its equation is of the form:
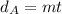
From the graph, we know that the distance is 300 when the time is 1, therefore:
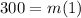
Solving

The equation is then:

For balloon B, we have a similar situation, therefore, the equation for B is:
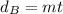
For the table, we know that when the distance is 590 then the time is 1, therefore, the equation is:
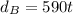
for balloon C, we have the equation:
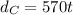
We are asked the following questions:
a) what is the rate of change of each ballon. Let's remember that for a line equation of the form:

The value of "m" is the rate of change. Therefore, the rate of change of each balloon is:
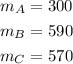
b) Which balloon is rising the slowest. The balloon that is rising the slowest is the one with the smallest rate of change, that is, balloon A.
c) How much each balloon rise in three seconds. To determine that we need to replace on the formula of each balloon the value for t = 3.
For balloon A, we have:

Replacing the value of t
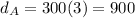
For balloon B,
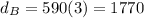
For balloon C
