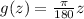Question

Recall that there are 2π radians in one full rotation and 360 degrees in one full rotation.Suppose an angle has a measure of 2.6 degrees.This angle (with a measure of 2.6 degrees) is what percent of a full rotation? ________%   Use your work in part (i) to determine the measure of the angle in radians. ________degrees   If an angle has a measure of z degrees, what is the measure of the angle in radians?__________ radians   Write a function gg that determines the radian measure of an angle in terms of the degree measure of the angle, z.g(z)=

Answer 1

Since a full rotation represents is 360° we find the percent 2.6° represents by using the rule of three:

`\begin{gathered} 360\rightarrow100 \\ 2.6\rightarrow x \end{gathered}`

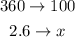
Then:

`x=(2.6\cdot100)/(360)=0.722`

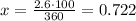
Therefore, 2.6° represents 0.722% of a full rotation.

To find out how many radians does 2.6° is we also use the rule of three:

`\begin{gathered} 360\rightarrow2\pi \\ 2.6\rightarrow x \end{gathered}`

then:

`x=(2.6\cdot2\pi)/(360)=0.045`

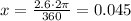
Therefore 2.6° is 0.045 radians.

Now, if an angle has a mesuare of z degrees we use once again the rule of three to find how many radians it is:

`\begin{gathered} 360\rightarrow2\pi \\ z\rightarrow x \end{gathered}`

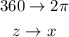
Then:

`x=(z\cdot2\pi)/(360)=(\pi z)/(180)`

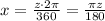
Therefore the angle z is:

`(\pi z)/(180)`

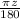
in radians.

To find the function we only use the result above, therefore we have:

`g(z)=(\pi)/(180)z`