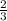Question

1 + logx = log(7x + 2)

Answer 1

Given the equation:

1 + logx = log(7x + 2)

Let's solve the equation for x.

To solve for x, aply the following steps:

Step 1:

Subtract logx from both sides

1 + logx - logx = log(7x + 2) - logx

1 = log(7x + 2) - logx

logx - log(7x + 2) = -1

Step 2:

Apply the quotient property of logarithms

`\log ((x)/(7x+2))=-1`

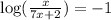
Step 3:

Rewrite log in exponential form

`(x)/(7x+2)=10^(-1)`

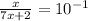
Step 4:

Cross multiply

`x=(7x+2)10^(-1)`

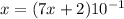
Step 5:

Simplify

`\begin{gathered} x=(7x+2)/(10) \\ \\ x=(7x)/(10)+(2)/(10) \\ \\ x=(7x)/(10)+(1)/(5) \\ \\ x-(7x)/(10)=(1)/(5) \\ \\ (10x-7x)/(10)=(1)/(5) \\ \\ (3x)/(10)=(1)/(5) \end{gathered}`

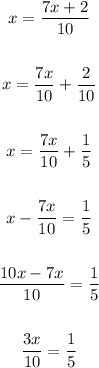
Solving further:

Cross multiply

`\begin{gathered} 3x(5)=10(1) \\ \\ 15x=10 \end{gathered}`

Divide both sides by 15:

`\begin{gathered} (15x)/(15)=(10)/(15) \\ \\ x=(2)/(3) \end{gathered}`

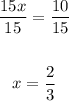
Therefore, the value of x is:

`(2)/(3)`

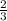
ANSWER:

`(2)/(3)`