Given the equation:
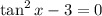
first let's move the -3 to the right side. Remember that when we do this, it must move with the opposite sign:
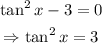
now we can apply the square root on both sides of the equation to get the following:
![\begin{gathered} \sqrt[]{\tan ^2x}=\sqrt[]{3} \\ \Rightarrow\tan x=\sqrt[]{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/nldqa1jcvgkdjkz58n1fup459wms9xl9m8.png)
next we use the inverse function of tangent to solve for x:
![\begin{gathered} \tan x=\sqrt[]{3} \\ \Rightarrow x=\tan ^(-1)(\sqrt[]{3})=60 \\ x=60 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/iqmp6uol8nmdtcs9vwoajsld9m9n1g2lhp.png)
therefore, x = 60