Given,
The angle of projection of the magma chunk, θ_D=35°
The time of flight, t=45 s
The height from which the magma chunk was projected, H=3.30 km=3300 m
The time of flight is given by,
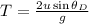
Where u is the initial velocity with which the Magna chunk was projected and g is the acceleration due to gravity.
On substituting the known values,
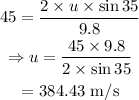
The range of the projectile or the horizontal distance traveled by the magma is given by,
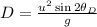
On substituting the known values,

Thus the magma travels for a horizontal distance of 14.17 km