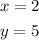Question

Solving systems of equations using substitution. x=7-y. x=-2y+12

Answer 1

The solution to the given system of equation is;

`\begin{gathered} x=2 \\ y=5 \end{gathered}`

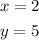
Step-by-step explanation:

Given the system of equation:

`\begin{gathered} x=7-y\text{ -----1} \\ x=-2y+12\text{ ----2} \end{gathered}`

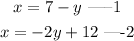
Let us make y the subject of formula in equation 1;

`\begin{gathered} x=7-y \\ y=7-x\text{ ----3} \end{gathered}`

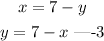
Let us substitute equation 3 into equation 2 and solve;

`\begin{gathered} x=-2y+12 \\ x=-2(7-x)+12 \\ x=-14+2x+12 \\ x=-14+12+2x \\ x=-2+2x \\ \text{collect the like terms;} \\ 2=2x-x \\ 2=x \\ x=2 \end{gathered}`

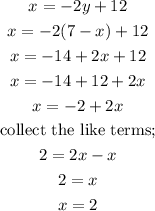
We can now substitute to get y;

using equation 3;

`\begin{gathered} y=7-x \\ y=7-2 \\ y=5 \end{gathered}`

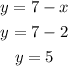
Therefore, the solution to the given system of equation is;

`\begin{gathered} x=2 \\ y=5 \end{gathered}`