Question

Two different families pay for entry into a water park.Family 1 has 2 adults and 3 children and costs a total of 20 pounds to enter the park.family 2 has 1 adult and 4 children and costs a total of 15 pounds to enter the park. Work out the cost of the adult ticket and the child ticket.

Answer 1

Let C represent children and let A represent adult tickets

Family 1 : 2A + 3C = 20

Family 2: A + 4C = 15

Let's solve the equation simultaneously:

2A + 3C = 20......................(1)

A + 4C = 15.......................(2)

From equation 2, make A the subject:

A = 15 - 4C

Now substitute (15 - 4C) for A in equation 1:

`2(15-4C)\text{ + 3C = 20}`
`30\text{ - 8C + 3C = 20}`
`30\text{ - 5C = 20}`

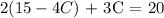
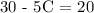
Now we have:

`5C\text{ = 30 - 20}`
`5C\text{ = 10}`

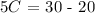
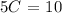
To find C, divide both sides by 5:

`(5C)/(5)\text{ = }(10)/(5)`
`C\text{ = 2}`

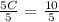
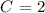
Now substitue 2 for C in equation 2:

A + 4(2) = 15

A + 8 = 15

subtract * from both sides:

A + 8 -8 = 15 -8

`A\text{ = 7}`

Therefore, the cost of adult ticket is 7 pounds and the cost of children ticket is 2 pounds