Answer:
equation;
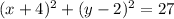
Center (-4,2)
Radius is

Explanation:
Since the x^2 and y^2 have the same coeffiecent this will be a circle in a form of
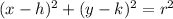
Where (h,k) is center
r is the radius
So first we group like Terms together
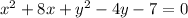
Add 7 to both sides


Since the orginal form of the equation of the circle has a perfect square we need to complete the square for each problem
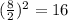
and
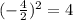
so we have
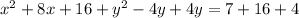
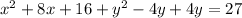
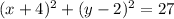
To find our center, h is -4 and k is 2
so the center is (-4,2)
The radius is
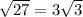
So the radius is 3 times sqr root of 3.