Question

I’m stuck on what equation I need to set up

Answer 1

The painting is a square, which means all its sides are equal.

If x is the length of one side, then, all the remaining 3 sides also have the same length: x.

The area of a square is the square if its side, then, for a square with sides x:

`\text{Area}=x\cdot x=x^2`

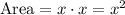
We know that the area of the painting will be 400 square inches, then:

a. The equation that can be set up to find the length of a side is:

`x^2=400in^2`

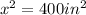
b. We can solve the equation by finding a number that multiplied by itself gives 400. For this case, we have two solutions. 20 and -20, since:

`20^2=20\cdot20=400`

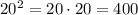
And:

`(-20)^2=(-20)\cdot(-20)=400`

-20 is also a solution because as a negative number, when multiplied by itself, gives a positive one. (A product between negative numbers gives always a positive number).

c. We have two solutions, however, only one of them makes sense: the 20. A negative length makes no sense, so we can discard the second solution (-20).

d. The length of the wood trim needed to go around the painting is then 20 inches. (we should not forget the units.)