Recall that an angle Θ:
1) Lies in quadrant 1 if Θ is coterminal to an angle between 0 and 90 degrees.
2) Lies in quadrant 2 if Θ is coterminal to an angle between 90 and 180 degrees.
3) Lies in quadrant 3 if Θ is coterminal to an angle between 180 and 270 degrees.
4) Lies in quadrant 4 if Θ is coterminal to an angle between 270 degrees and 360 degrees.
Now, recall that Θ and Θ+360 degrees are coterminal angles.
Notice that:
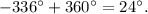
Since:
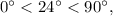
and -336 degrees is coterminal to 24 degrees, then -336 degrees lies on quadrant I.
Answer: Option B.