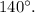Recall that the interior angles of a regular quadrilateral add up to 360 degrees, and a right angle has a measure of 90 degrees.
Let x° be the measure of the fourth angle, then we can set the following equation:
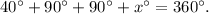
Adding like terms we get:
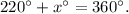
Subtracting 220 degrees from the above result we get:
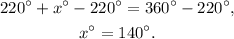
Answer: