The Scalar and Cross Product of Vectors
Given two vectors:
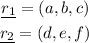
The scalar product is defined as:

The cross product is the result of computing the following determinant:
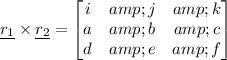
Where i, j, and k are the unit vectors in each of the directions x, y, and z, respectively.
This concept will be applied to the following physics problem.
Given a force F= (2, 3, 0) and the distance vector d = (4, 0, 0), the torque is defined by:

Calculating:
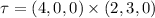
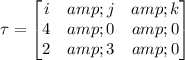
Calculating the determinant:
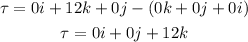
Expressing in vector form τ = (0, 0, 12) <= should use angle brackets
The magnitude of the torque is:
![\begin{gathered} |\tau|=\sqrt[]{0^2+0^2+12^2} \\ |\tau|=\sqrt[]{144} \\ |\tau|=12 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/mioic3llp7hl77zfkbcajx6exnyf6ug04p.png)
The power P is equal to the scalar product of the torque by the angular velocity w. We are given the angular velocity w = (3, 3, 2), thus:
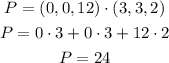
P = 24