Question

Just 34 unless you want to help me with more?

Answer 1

M is the midpoint of the line segment FG.

Being the midpoint means that M divides the line in two equal halves so you know that the distance between F and M is equal to the distance between M and G, symbolically:

FM=MG

And of you add them you'll be able to calculate the length of the whole line FG

34.

Given the expressions

FM= 5y+13

MG=5-3y

We know that FM=MG, so the first step is to replace this equivalency with the given expressions. This way you'll determine an equation with one unknown y.

Once you have the equation you can clear the value of y:

`\begin{gathered} FM=MG \\ 5y+13=5-3y \end{gathered}`

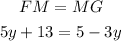
Pass all terms with the unknown to one side of the equation and all others to the other side:

`\begin{gathered} 5y+3y=5-13 \\ 8y=-8 \\ y=-1 \end{gathered}`

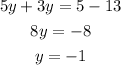
y=-1

Now that you know the value of y, you can replace it in the given expressions to calculate the length of FG

`\begin{gathered} FG=FM+MG \\ FG=(5y+13)+(5-3y) \\ FG=5y+13+5-3y \\ FG=2y+18 \\ \text{Replace with y=-1} \\ FG=2(-1)+18 \\ FG=16 \end{gathered}`

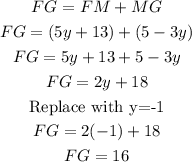
The length of the line segment FG is 16 units.