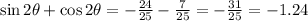Question

If theta is in quadrant II and cos theta= -3/5, what is sin 2 theta + cos 2 theta?

Answer 1

sin(2θ) + cos(2θ) = -31/25 = -1.24

Step-by-step explanation

If we do the inverse of the cosine to -3/5 we would get the angle θ. Then we can know the value of the sine:

`\sin \theta=\sin (\cos ^(-1)(-(3)/(5)))=(4)/(5)`

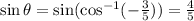
So we have:

• sin(θ) = 4/5

,

• cos(θ) = -3/5

To find sin(2θ) + cos(2θ) we'll have to use the trigonometric identities:

`\begin{gathered} \sin 2\theta=2\sin \theta\cos \theta \\ \cos 2\theta=1-2\sin ^2\theta \end{gathered}`

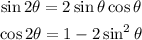
Since we have the sine and cosine of theta, we can solve this:

`\sin 2\theta=2\cdot(4)/(5)\cdot(-(3)/(5))=-(24)/(25)`
`\cos 2\theta=1-2((4)/(5))^2=1-2\cdot(16)/(25)=1-(32)/(25)=-(7)/(25)`

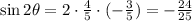
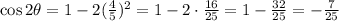
The sum is:

`\sin 2\theta+\cos 2\theta=-(24)/(25)-(7)/(25)=-(31)/(25)=-1.24`