we have that
B=5 degrees
C=125 degrees
b=200 units
step 1
Find out the measure of angle A
Remember that
the sum of the interior angles in any triangle must be equal to 180 degrees
so
A+B+C=180
substitute given values
A+5+125=180
A=180-130
A=50 degrees
step 2
Applying the law of sines
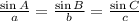
Find out the value of a
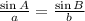
substitute given values
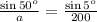
solve for a
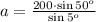
a=1,757.9 units
step 3
Find out the value of c
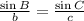
substitute given values
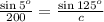
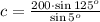
c=1,879.7 units