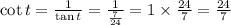Question

the angle t is an acute angle and sin t and cost t are given. Use identities to find tan t , csc t, sec t, and cot t. where necessary, rationalize demonstrations.sin t= 7/25, cos t= 24/25

Answer 1

tan t = 7/24

csc t = 25/7

sec t = 25/24

cot t = 24/7

Step-by-step explanation:

From the question, we're told that sin t = 7/25 and cos t = 24/25. Since we know the identities of sine and cosine to be as follows we can go ahead and determine tan t as shown below;

`\begin{gathered} \sin t=\frac{opposite}{\text{hypotenuse}}=(7)/(25) \\ \cos t=\frac{adjacent}{\text{hypotenuse}}=(24)/(25) \\ \therefore\tan t=\frac{opposite}{\text{adjacent}}=(7)/(24) \end{gathered}`

Let's go ahead and find cosecant t (csc t);

`\csc t=(1)/(\sin t)=(1)/((7)/(25))=1*(25)/(7)=(25)/(7)`

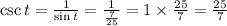
For sec t, we'll have;

`\sec t=(1)/(\cos t)=(1)/((24)/(25))=1*(25)/(24)=(25)/(24)`

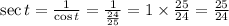
For cot t;

`\cot t=(1)/(\tan t)=(1)/((7)/(24))=1*(24)/(7)=(24)/(7)`