Choose two consecutive points on the graph and find the rate of change.
We will start with t = 1000 and t = 1500:
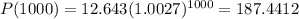
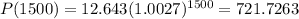
Remember that the rate of change is found by the difference in y over the difference in x.
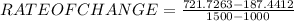
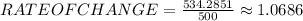
Let's do it now for t = 1500 and t = 2000.
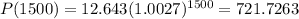
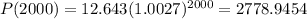
In this case the rate of change would be:
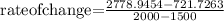
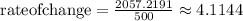
The slopes are different and due to the type of function they will always increase when taking larger values.