Answer:

Explanations:
Given the function
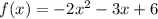
We are to look for the difference quotient:
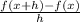
Get f(x + h)
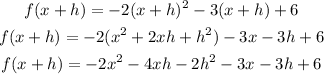
Given f(x) expressed as:
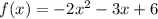
Substitute both functions into the difference quotient;

Factor out "h" from the result to have

This shows that the simplified form of the expression is -4x - 2h - 3