Question

The sum of the squares of three consecutive odd numbers is 83. Find the numbers.

Answer 1

In order to represent three consecutive odd numbers, we can use the expressions "x", "x+2" and "x+4".

If we add the square of each number, the result is 83, so we can write the following inequality:

`\begin{gathered} x^2+(x+2)^2+(x+4)^2=83\\ \\ x^2+x^2+4x+4+x^2+8x+16=83\\ \\ 3x^2+12x+20=83\\ \\ 3x^2+12-63=0\\ \\ x^2+4x-21=0 \end{gathered}`

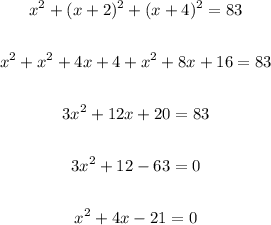
Let's solve this quadratic equation using the quadratic formula, with a = 1, b = 4 and c = -21:

`\begin{gathered} x=(-b\pm√(b^2-4a)c)/(2a)\\ \\ x=(-4\pm√(16+84))/(2)\\ \\ x=(-4\pm10)/(2)\\ \\ x_1=(-4+10)/(2)=(6)/(2)=3\\ \\ x_2=(-4-10)/(2)=(-14)/(2)=-7 \end{gathered}`

If we assume the numbers are positive, the numbers are 3, 5 and 7.

(The other result, with negative numbers, would be -7, -5 and -3).