Question

for any numbers x,y [x=0 in(4) and y = 0 in (5)] and any positive integers m,n, the following holds:x^m · x^n=x^m+nProve number 1

Answer 1

Proved

Step-by-step explanation:

To prove x^m · x^n=x^m+n, let's assign numbers to x, m and n

let x = 2

m = 3, n = 4

x^m · x^n = 2^3 . 2^4

x^m+n = 2^(3+4)

Solve each of the above seperately and comparew the answer:

`\begin{gathered} x^m* x^n=2^3*2^4 \\ =\text{ (2}*2*2)*(2*2*2*2) \\ =\text{ 8}*16 \\ =\text{ }128 \end{gathered}`
`\begin{gathered} x^(m+n)=2^(3+4) \\ =2^7\text{ = 2}*2*2*2*2*2*2 \\ =\text{ 128} \end{gathered}`
`\begin{gathered} sincex^m* x^n\text{ = 128} \\ \text{and x}^(m+n)\text{ = 128} \\ \text{Therefore, }x^m* x^n\text{ = x}^(m+n) \end{gathered}`

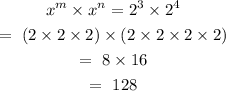
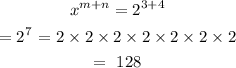
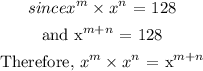
This expression x^m · x^n=x^m+n has been proved to be equal