Step-by-step explanation
To solve this question, we can use the empirical rule
The empirical rule, also referred to as the three-sigma rule or 68-95-99.7 rule, is a statistical rule which states that for a normal distribution.
So if the mean is 13.9 and the standard deviation is 2.6
Then to obtain 8.7, there must have been 2 standard deviations below the mean. That is:
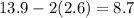
From the above, we can see that the per cent that will be less than 2 standard deviations below the mean is approximately
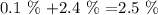
Thus, about 2.5% will be less than 8.7