Question

how many solutions does the following system have and if any what is the solution. If there are solution, find the solution.

Answer 1

`t(x)=-(2)/(3)x+1`
`s(x)=(4)/(5)x+(4)/(15)`

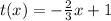
When you have a swystem of lineal equation, you can find the number of solutios knowing the value of the slope (m) in each equation:

If both slopes are the same there are no solution. (m1=m2)

If the slopes are different there are one solution. (m1≠m2)

If the eqations are the same there are infinite solutions. (f(x)=g(x))

You can identify the slope (m) in a lineal equation in slope-intercept form (y=mx+b) as the coeffient of the x (the number on the left of the x).

The slope in t(x) is -2/3

The slope in s(x) is 4/5

As the slopes are different adn the equation also are different there are one solution.

To find the solution of a system of lineal equations you equal the equations:

In this case:

`t(x)=s(x)`
`-(2)/(3)x+1=(4)/(5)x+(4)/(15)`

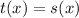
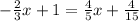
You clear the x and the value you get is the solution:

`-(2)/(3)x+1-1=(4)/(5)x+(4)/(15)-1`
`-(2)/(3)x=(4)/(5)x+((4-15)/(15))`
`-(2)/(3)x=(4)/(5)x-(11)/(15)`
`-(2)/(3)x-(4)/(5)x=(4)/(5)x-(4)/(5)x-(11)/(15)`
`((-10-12)/(15))x=-(11)/(15)`
`-(22)/(15)x=-(11)/(15)`
`(-(15)/(22))(-(22)/(15)x)=(-(15)/(22))(-(11)/(15))`
`x=(11)/(22)=0.5`

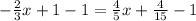
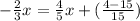
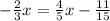
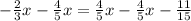
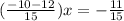
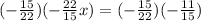
You can use the value of x to find the y coordinate of the solution.

`y=-(2)/(3)(0.5)+1`
`y=-(1)/(3)+1=(-1+3)/(3)=(2)/(3)=0.66`

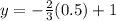
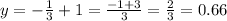
then, the solution is x=0.5 and the coordinates of the solution are:

(0.5 , 0.66)