Question

Solve the system of equations: 2x+y+2z=16 x+3y−z=37 4x−y+3z=4

Answer 1

Hello there. To solve this question, we have to remember some properties about system of equations.

Given the following system of linear equations:

`\begin{cases}2x+y+2z=16\\x+3y-z=37\\4x-y+3z=4\end{cases}`

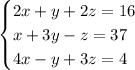
We'll rewrite it in the form of augmented matrix:

`\begin{bmatrix}\begin{array}c2 & 1 & 2 & 16 \\ 1 & 3 & -1 & 37 \\ 4 & -1 & 3 & 4\end{array} \end{bmatrix}`

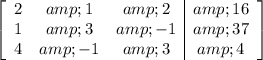
Now, we want to find the row-echelon form of this system, that is, we'll multiply the equations by a factor in order to find an equivalent system and we can solve it for each of the variables separately.

Divide the first equation by a factor of 2, getting:

`\begin{bmatrix}\begin{array}c1 & (1)/(2) & 1 & 8 \\ 1 & 3 & -1 & 37 \\ 4 & -1 & 3 & 4\end{array}\end{bmatrix}`

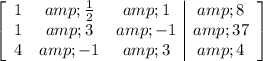
Multiply the first equation by a factor of (-1) and add it to the second equation. This happens because we chose the factor under the first term as the pivot for the second line.

`\begin{bmatrix}\begin{array}ccc1 & (1)/(2) & 1 & 8 \\ 0 & (5)/(2) & -2 & 29 \\ 4 & -1 & 3 & 4\end{array}\end{bmatrix}`

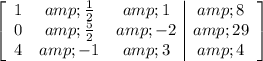
Next, multiply the first equation by a factor of (-4) and add it to the third equation

`\begin{bmatrix}\begin{array}ccc1 & (1)/(2) & 1 & 8 \\ 0 & (5)/(2) & -2 & 29 \\ 0 & -3 & -1 & -28\end{array}\end{bmatrix}`

Now, we move to the second equation. Choosing the element a22 as the pivot, we have to multiply the second equation by a factor of 6/5 and add it to the third equation:

`\begin{bmatrix}\begin{array}c1 & (1)/(2) & 1 & 8 \\ 0 & (5)/(2) & -2 & 29 \\ 0 & 0 & -(17)/(5) & (34)/(5)\end{array}\end{bmatrix}`

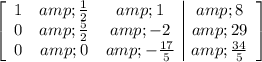
Back into the system of equations form, we have

`\begin{cases}x+(1)/(2)y+z=8 \\ \\ (5)/(2)y-2z=29 \\ \\ -(17)/(5)z=(34)/(5)\end{cases}`

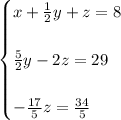
Solving for z, we get

`-(17)/(5)z=(34)/(5)\Rightarrow z=-2`

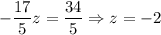
Plugging it into the second equation, we get

`\begin{gathered} (5)/(2)y-2\cdot(-2)=29 \\ \\ (5)/(2)y=25 \\ \\ \Rightarrow y=10 \end{gathered}`

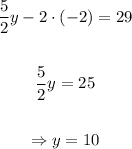
Finally, plugging it in the first equation, we find

`\begin{gathered} x+(1)/(2)\cdot10-2=8 \\ \\ \Rightarrow x=5 \end{gathered}`

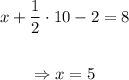
Therefore the solution to this system of equations is:

`S=\{(x,\,y,\,z)\in\mathbb{R}^3|(x,\,y,\,z)=(5,\,10,\,-2)\}`

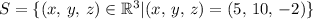
This is the final answer to this question.