Question

8. The lengths of pregnancies are normally distributed with a mean of 268 days and a standarddeviation of 15 days. Find the probability of a pregnancy lasting 292 days or longer.

Answer 1

From the problem we have :

`\begin{gathered} \bar{x}=268 \\ \sigma=15 \end{gathered}`

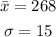
Graphically the normal distribution would look like the following

To calculate the value of the probability that a pregnancy will be ad 292 or more days use the table z with its equation

`\begin{gathered} Z=\frac{X-\bar{x}}{\sigma} \\ X=292 \\ Z=(292-268)/(15) \\ Z=(24)/(5) \\ Z=1.6 \end{gathered}`

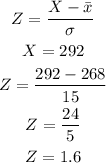
To calculate the probability we have to find the value of Z in the table:

`P(x\ge292)=1-P(x\le292)`

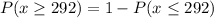
from table Z we know that

`\begin{gathered} P(x\le292)=Z_(1.6) \\ P(x\le292)=0.9452 \end{gathered}`
`\begin{gathered} P(x\ge292)=1-P(x\le292) \\ P(x\ge292)=1-1.9452 \\ P(x\ge292)=0.548 \end{gathered}`

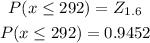
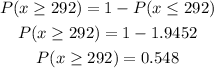
The probability that a pregnancy lasts 292 or more days is 5.5%