Question

At a carnival, there is a game where you can draw one of 50 balls from a bucket if you pay $8. The balls are numbered from 1 to 50. If the number on the ball is even, you win $10. If the number on the ball is odd, you win nothing. If you play the game, what is the expected profit?

Answer 1

Expected Value of a Random Variable

Given a random variable with values:

X={x1,x2,x3,...xn}

with probabilities of:

P={p1,p2,p3,...pn}

The expected value is:

`Ex=\sum ^n_1x_i\cdot p_i`

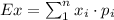
There are two probable events: the ball has an even number or the ball has an odd number. They are numbered from 1 to 50, thus there are 25 even-numbered and 25 odd-numbered balls.

If the number is even, you win $10, if the number is odd, you win nothing, thus:

X={10,0}

Assuming the first value is for even-numbered balls

The probability of each event is exactly the same (0.5):

P={0.5,0.5}

The expected value is:

Ex = 10*0.5 + 0*0.5

Ex = $5

Since you had to pay $8 to draw the ball, your expected profit is $5 - $8 = -$3.

This means you expect to lose $3.