Question

You have been asked to find the inverse off (x) = 3 + V X - 1. What would your first step be?A Square both sides of the equation.Add 1 to both sides of the equation.Subtract 3 from both sides of the equation.Take the square root of both sides.

Answer 1

We are given a function that is defined by a single variable ( x ) as follows:

`f\text{ ( x ) = 3 + }\sqrt{x\text{ - 1}}`

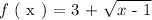
We are asked to find an inverse of the given function f ( x ) defined above.

We recall that an inverse of a function is defined as reflection of function f ( x ) across a line defined as:

`y=x`

Mathematically, we can find the inverse if the function is defined as an equation.

The process of finding an inverse carries two steps:

First step: Make ( x ) the subject of the formula.

Before we start makking ( x ) the subject, we will make the following substitution.

`y\text{ = f ( x )}`

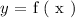
We replace the above substitution into the function given:

`y=\text{ 3 + }\sqrt{x\text{ - 1}}`

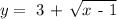
Now to make ( x ) the subject we will isolate the variable ( x ). We see that the variable ( x ) is accompained by a constant ( 1 ) under the root. We wil first isolate this entire root on the right hand side of the "=" sign.

We do this by subtracting ( 3 ) from both sides of the equation:

`\begin{gathered} \text{ y - 3 = 3 +}\sqrt{x\text{ - 1}}\text{ - 3 } \\ \textcolor{#FF7968}{y}\text{\textcolor{#FF7968}{ - 3 = }}\textcolor{#FF7968}{\sqrt{x\text{ - 1}}} \end{gathered}`

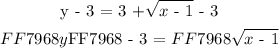
Then we need to remove the radiacal ( root ) sign from over the head of our subject variable ( x ). We will do this by taking squares on both sides of the equation:

`\begin{gathered} (y-3)^2\text{ = \lbrack }√(x-1)\rbrack^2 \\ \textcolor{#FF7968}{(y-3)^2}\text{\textcolor{#FF7968}{ = x - 1}} \end{gathered}`

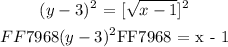
Then we will add ( 1 ) on both sides of the equation to isolate the variable ( x ):

`\begin{gathered} (y-3)^2\text{ +1 = x - 1 + 1} \\ \textcolor{#FF7968}{(y-3)^2}\text{\textcolor{#FF7968}{ +1 = x }} \end{gathered}`

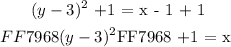
We have finally made the variable ( x ) the subject of the equation.

Step 2: Substitute y = x

In this step we will make the substitution of line of reflection ( y = x ). We do this by interchanging all ( x ) with ( y ) and all ( y ) with ( x ):

`(x-3)^2\text{ + 1 = y}`

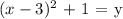
Then we will express the inverse in standard notation:

`y=f^(-1)(\text{ x )}`

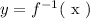
Therefore,

`\textcolor{#FF7968}{f^(-1)(x)=(x-3)^2}\text{\textcolor{#FF7968}{ + 1}}`

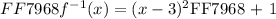
Answer: The first mathematical operation in finding the inverse was " Subtract ( 3 ) from both sides of the equation "