Question

Suppose the men's and women's winners, Joey and Miki, decide to compete against each other. To make the competition more interesting, Joey will not start until Miki has eaten 15 hot dogs. Assume that Joey and Miki eat at a constant rate throughout the competition. Based on the number of hot dogs eaten in 10 minutes by Joey (75) and Miki (48.5),how many minutes after Joey starts eating will they have eaten the same number of hot dogs? 1. Write an expression for the number of hot dogs Joey and Miki will have eaten m minutes after Joey starts. 2. Write an equation to represent when Joey and Miki will have eaten the same number of hot dogs. Solve the equation and interpret the solution.

Answer 1

The first step is to find the minutes passed when Joey starts eating:

To do this you have to find the number of hot dogs that Miki eats in one minute:

Do a proportion:

Miki eats 48.5 hot dogs in 10 minutes, translate this to 1 minute

`(48.5)/(10)=4.85\text{ hot dogs per minute}`

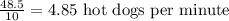
Now with this rate calculate how many minutes have passed when Miki has eaten 15 hot dogs:

`15hd*(1min)/(4.85hd)=3.09\cong3min`

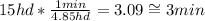
Now calculate the total rate between both:

`48.5+75=123.5\text{ hot dogs in 10 minutes}`

the slope of the equation will be:

`(123.5)/(10)=12.35`

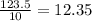
1. So formulate the equation for the hot dog's number:

`hd=12.35m+15`

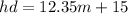
2. Now formulate two new equations, one for Joey and one for Miki:

`J=7.5m`
`M=4.85m+15`

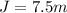
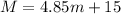
Equalize the equations:

`7.5m=4.85m+15`

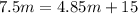
Solve:

`7.5m-4.85m=15`
`2.65m=15`
`m=(15)/(2.65)=5.66\text{ min}`

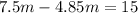
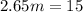
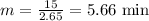
That means that Joey and Miki will have eaten the same number of hot dogs 5.66 min after Joey started eating, or if you add the 3.09 min that Miki delayed in eating 15 hot dogs, you can conclude that Joey and Miki will have eaten the same number of hot dogs after 8.75 min.