Answer:
8 and -4
Explanation:
Solving The Equation Geometrically/Visually:
By definition the distance between two numbers is always positive. So we can look 6 units to the right of 2, as well as 6 units to the left of 2, and we should get two numbers who both have a distance of 6 units.
I uploaded an image which you can refer to, which visually shows what going to the right and left 6 units does. Using this diagram we can derive the two answers: 8 and -4
Solving The Equation Algebraically:
The distance between two numbers in general can be found, by taking the absolute value of the difference of the numbers:
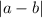 , which should give you the distance between the numbers "a" and "b"
, which should give you the distance between the numbers "a" and "b"
The order in which we set up "a" and "b" doesn't matter, we could do:
 and get the same result, which we can prove by factoring out negative one, giving you:
and get the same result, which we can prove by factoring out negative one, giving you:
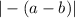 , and by definition the absolute value will get rid of this negative, giving us our original equation:
, and by definition the absolute value will get rid of this negative, giving us our original equation:
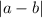 , so the order does not matter.
, so the order does not matter.
So using this formula we can set up the equation:

By definition of an absolute value, the
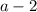 could equal negative six, or positive six, since the absolute value of those two numbers are the same.
could equal negative six, or positive six, since the absolute value of those two numbers are the same.
Let's look at the first solution, where
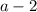 is positive six
is positive six
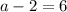
add 2 to both sides
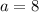
This is one of our solutions!
Now let's look at the other solution, where
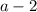 is negative six
is negative six
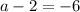
Add 2 to both sides

As you can see we get the same solution as the one we got from solving it geometrically! This question is not quite complex so it can be solved visually without much difficulty, although it is very useful to solve this algebraically when looking at numbers with greater distances.