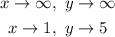Given
The function,
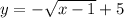
To find:
The end behaviour of the function.
Step-by-step explanation:
It is given that,
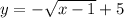
And, the graph of the above function is,
That implies,
From the graph,
As x tends to 1,
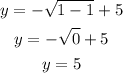
Also,
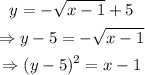
Then,
As x tends to infinity,
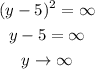
Hence, the answer is option C),