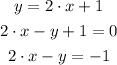We need to determine the equation of a line in three forms. The standard expression for this forms can be seen below:

Where (x1,y1) is a point that belongs to the line, m is the slope and b is the y-intercept. The slope can be calculated with two known points using the following expression:

With this we can find the three equations. To begin we will calculate the slope:
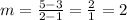
Then we can determine the point-slope form using the point (1,3).
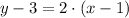
To determine the slope-intercept form we will use the form above and isolate the y variable on the left side.
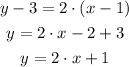
Finally we can determine the standard form by isolating the constant on the right side.