The identity of the sum of cos two angles is
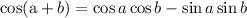
Since the given expression is
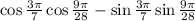
Compare it with the identity above
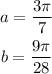
Then the expression can be written as cos (a + b)
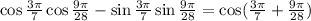
To add the 2 angles equalize their denominators by finding LCM of them
Since LCM of 7 and 28 is 28, then
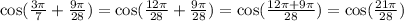
Now we need to find cos (21pi/28)
Since the angle of measures 21pi/28 = 3pi/4 in its simplest form
Since the angle 3pi/4 is greater than pi/2 and pi, then it lies in the second quadrant
The measure of any angle in the second quadrant is between pi/2 and pi, and the value of cos any angle in the second quadrant is negative
![\begin{gathered} \cos ((3\pi)/(4))=-\cos (\pi)/(4) \\ \cos (\pi)/(4)=\frac{\sqrt[]{2}}{2} \\ \cos (3\pi)/(4)=-\frac{\sqrt[]{2}}{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/hwdd4tfmhapbhr3wooy8r3cajvchglwdt2.png)
The answer is
![-\frac{\sqrt[]{2}}{2}OR-\frac{1}{\sqrt[]{2}}](https://img.qammunity.org/2023/formulas/mathematics/college/rtysnx9mml4as7fex0twopqpaelv0a498r.png)