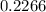Given that the probability that Joe burns dinner is:
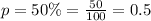
You need to use the following Binomial Distribution Formula, in order to solve the exercise:
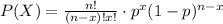
Where "n" is the sample size, "x" is the number of successes desired, and "p" is the probability of getting a success in a trial.
(a) You must find the probability that in the next 7 dinners Joe prepares, 4 of them will burn. Therefore, for this case:
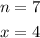
Then, you can substitute values into the formula and evaluate:

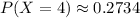
(b) You must find the probability that in the next 7 dinners Joe prepares, at least 5 of them will burn. Therefore, since "at least" indicates greater than or equal to 5, you need to set up this Sum for:
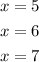
Then:
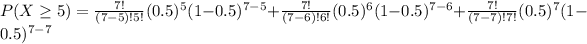
Evaluating, you get:
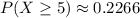
(c) You must find the probability that in the next 7 dinners Joe prepares, less than 3 of them will burn. Therefore, you need to set up a Sum for:

As follows:

Evaluating, you get:

Hence, the answers are:
(a)
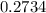
(b)
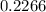
(c)