Question

Americans receive an average of 17 Christmas cards each year. Suppose the number of Christmas cards is normally distributed with a standard deviation of 6. Let X be the number of Christmas cards received by a randomly selected American. Round all answers to 4 decimal places where possible.a. What is the distribution of X? X ~ N(,)b. If an American is randomly chosen, find the probability that this American will receive no more than 16 Christmas cards this year. c. If an American is randomly chosen, find the probability that this American will receive between 20 and 26 Christmas cards this year. d. 67% of all Americans receive at most how many Christmas cards? (Please enter a whole number)

Answer 1

Part a.

From the given information, we know that

`\begin{gathered} \mu=17 \\ \sigma=6 \end{gathered}`

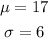
Then, the distribution of X

`\begin{equation*} N(\mu,\sigma) \end{equation*}`

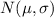
is given by:

`N(17,6)`

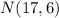
Part b.

In this case, the measure X is equal to 16, then the corresponding z-score

`z=(X-\mu)/(\sigma)`

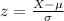
is given by

`\begin{gathered} z=(16-17)/(6) \\ then \\ z=-0.16666 \end{gathered}`

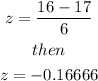
Since in order to find the probability to receive no more than 16 Christmas cards, we need to find the following probability:

`P(X<16)`

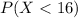
or equivalently,

`P(z<-0.1666)`

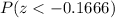
Then, from the corresponding z-table, this value corresponds to 0.43382:

Therefore, the answer for part b is 0.43382.

Part c.

In this case, we need to find the following probability

So we need to find the probability:

Then, from the z value formula

`z=(X-\mu)/(\sigma)`

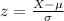
we have

`0.43991=(X-17)/(6)`

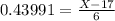
and we need to isolate the number of card X. Then, by multipying both sides by 6, we obtain

`2.63946=X-17`

then X is given by

`\begin{gathered} X=17+2.63946 \\ X=19.63946 \end{gathered}`

Therefore, by rounding to the nearest whole number, the answer for part d is 20 Christmas cards.