Question

QuestionThe following datavalues represent the daily amount spent by a family during a 7 day summer vacation.Find the population standard deviation of this dataset:$96, $125, $80, $110, $75, $100, $121(Round your answer to 1 decimal place).

Answer 1

17.7

Step-by-step explanation:

Given the dataset:

$96, $125, $80, $110, $75, $100, $121

To find the population standard deviation, use the formula:

`\sigma=\sqrt{(\sum\left(x_(i)-\mu\right)^(2))/(N)}`

Step 1: Find the mean

`\begin{gathered} \text{Mean,}\mu=(96+125+80+110+75+100+121)/(7) \\ =(707)/(7) \\ =101 \end{gathered}`

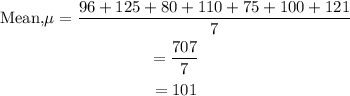
Step 2: Subtract the mean from each data point, square it and add them up:

`\begin{gathered} (96-101)^2+(125-101)^2+(80-101)^2+(110-101)^2 \\ ^{}+\mleft(75-101\mright)^2+\mleft(100-101\mright)^2+\mleft(121-101\mright)^2 \\ =25+576+441+81+676+1+400 \\ \sum (x_i-\mu)^2=2200 \end{gathered}`

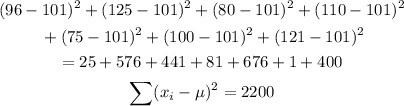
Step 3: Divide the sum by the number of data points in the population. The result is called the variance.

`(\sum(x_i-\mu)^2)/(N)=(2200)/(7)`

Step 4: Take the square root of the variance to get the standard deviation.

`\begin{gathered} \sigma=\sqrt[]{(2200)/(7)} \\ \sigma=17.7\text{ (to 1 decimal place)} \end{gathered}`