Question

A car travels 10 km southeast and

then 15 km in a direction 60° north of
east. Find the magnitude of the car's
resultant vector.
[?] km
Round to the nearest tenth.

Answer 1

`\bold{\huge{\green{\underline{Solution}}}}`

• A car travels 10 km southeast and then 15 km in a direction 60° north of east

`\bold{\underline{ To\: Find }}`

• We have to find the magnitude of the car of resultant vector

`\bold{\underline{ Let's \: Begin }}`

Here,

• In South east, car travels = 10km

• In North of east, it travels = 15km

• Angle between south east and north east is 60°

Therefore,

According to parallelogram law of resultant vector

If two vectors are represented by two adjacent sides of a parallelogram drawn from a point , the their resultant is equal to the diagonal of the parallelogram.

That is,

`\sf{ R = AC^(2)= A^(2)+ B^(2)}`

But, we have to calculate the magnitude of the resultant vector

`\sf{ | R |= √A^(2)+ B^(2)+ 2ABCos{\theta} }`

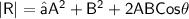
Subsitute the required values,

`\sf{ | R |=\sqrt{ (10)^(2) + (15)^(2) + 2× 10 × 15 × cos 60{\degree}}}`

`\sf =√( 100 + 225 + 20 × 15 × 1/2)`

`\sf`

`\sf R`

`\sf R`

`\sf{\red R }`

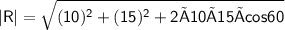
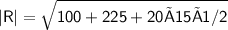
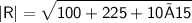
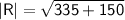
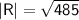
Hence, The magnitude of the car resultant vector is 22.02 km.