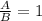Question

Let A be the area of a triangle with sides of length 25,35 and 30.Let B be the area of a triangle with sides of length 25,25, and 40.Find A/BDraw diagrams to represent the two triangles and label them with their dimensions. Use the formula for the area of a triangle to find A and B. Use PYTHAGOREAN Theorem

Answer 1

`(A)/(B)=1`

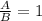
Step-by-step explanation:

Given that the triangle with area A has side length 25,25,30

And Triangle with Area B has side length 25,25,40.

Let us sketch the triangle below;

From the image of A and B;

The height of A is a, and that of B is b;

Recall that the area of a triangle can be calculated using the formula;

`\text{Area=}(1)/(2)bh`

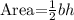
where b is base length and h is height.

Using Pythagorean theorem, let us calculate length of the heights a and b;

`\begin{gathered} c^2=a^2+b^2^{} \\ b^2=c^2-a^2 \\ b=\sqrt[]{c^2-a^2} \end{gathered}`

substituting for each triangle;

`\begin{gathered} a=\sqrt[]{25^2-15^2} \\ a=\sqrt[]{400} \\ a=20 \end{gathered}`
`\begin{gathered} b=\sqrt[]{25^2-20^2} \\ b=\sqrt[]{225} \\ b=15 \end{gathered}`

So, the area A and B will be;

`\begin{gathered} A=(1)/(2)bh \\ A=(1)/(2)*30*20 \\ A=300\text{ square units} \end{gathered}`
`\begin{gathered} B=(1)/(2)*40*15 \\ B=300\text{ square units} \end{gathered}`

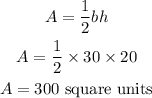
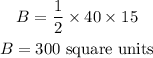
the ratio A/B is;

`(A)/(B)=(300)/(300)=1`

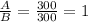
Therefore;

`(A)/(B)=1`