Question

find slope of the altitude on each side of triangle ABC (d) A(-2,-3), B(3,6), C(-5,5)letter d) question 3)

Answer 1

Graphing the points that make up the triangle you have

Now, to obtain the slope of each side of the triangle you can use the slope formula, that is,

`\begin{gathered} m=(y_(2)-y_(1))/(x_(2)-x_(1)) \\ \text{ Where m is the slope of the line and} \\ (x_1,y_1),(x_2,y_2)\text{ are two points through which the line passes} \end{gathered}`

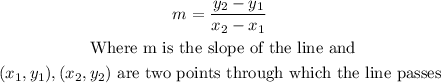
So, the slope of segment AB will be

`\begin{gathered} A=(x_1,y_1)=(-2,-3) \\ B=(x_2,y_2)=(3,6) \end{gathered}`
`\begin{gathered} m=(6-(-3))/(3-(-2)) \\ m=(6+3)/(3+2) \\ m=(9)/(5) \end{gathered}`

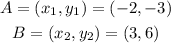
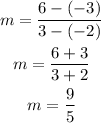
The slope of segment BC will be

`\begin{gathered} B=(x_1,y_1)=(3,6) \\ C=(x_2,y_2)=(-5,5) \\ m=(5-6)/(-5-3) \\ m=(-1)/(-8) \\ m=(1)/(8) \end{gathered}`

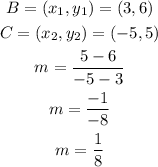
The slope of segment AC will be

`\begin{gathered} A=(x_1,y_1)=(-2,-3) \\ C=(x_2,y_2)=(-5,5) \\ m=(5-(-3))/(-5-(-2)) \\ m=(5+3)/(-5+2) \\ m=(8)/(-3) \\ m=-(8)/(3) \end{gathered}`

Therefore, the slope of each side of the triangle ABC is

`\begin{gathered} \text{ The slope of segment AB is }(9)/(5) \\ \text{ The slope of segment BC is }(1)/(8) \\ \text{ The slope of segment AC is }(-8)/(3) \end{gathered}`