Question

Bethany has $2.80 in quarters and dimes. The number of Dimes is 7 less than the number of quarters. Find the number of each kind of coin that she has

Answer 1

Let be "q" the number of quarters Bethany has and "d" the number of dimes she has.

You know that 1 quarter is $0.25 and 1 dime is $0.10. Then, since Bethany has $2.80 in quarters and dimes, you can set up the following equation:

`0.25q+0.10d=2.80`

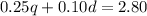
Knowing that the number of dimes is 7 less than the number of quarters, you can set up the second equation:

`d=q-7`

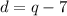
Then you have the following System of equations:

`\mleft\{\begin{aligned}0.25q+0.10d=2.80 \\ d=q-7\end{aligned}\mright.`

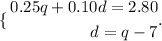
In order to solve it, you can use the Substitution method:

1. Substitute the second equation into the first equation.

2. Solve for "q".

Then:

`\begin{gathered} 0.25q+0.10d=2.80 \\ 0.25q+0.10(q-7)=2.80 \\ 0.25q+0.10q-0.7=2.80 \\ 0.35q=2.80+0.7 \\ q=(3.5)/(0.35) \\ q=10 \end{gathered}`

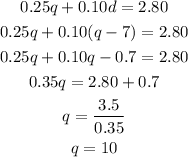
3. Substitute the value of "q" into the second equation and evaluate, in order to find the value of "d":

`\begin{gathered} d=q-7 \\ d=10-7 \\ d=3 \end{gathered}`

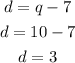
The answer is:

- Number of dimes: 3

- Number of quarters: 10