Question

The estimated length of a bolt is 4.75 inches. A machinist makes a bolt that is actually 4.769 inches. What is the percent error in the length of the bolt? (round your answer to the nearest tenth)

Answer 1

We are given that the exact value for the length of a bolt is 4.75 in. If the final measure is 4.769 then we can find the percentage of error by applying the following formula:

`N_{\text{final}}=N_{\text{real}}+N_{\text{real}}((x)/(100))`

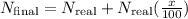
Where "x" is the error. Now we solve for "x". First by subtracting N real on both sides, like this:

`N_{\text{final}}-N_{\text{real}}=N_{\text{real}}((x)/(100))`

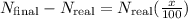
Now we divide by N real

`\frac{N_{\text{ final}}-N_(real)}{N_(real)}=(x)/(100)`

Now we multiply by 100 both sides:

`\frac{N_{\text{ final}}-N_(real)}{N_(real)}*100=x`

Replacing the values:

`(4.769-4.75)/(4.75)*100=x`

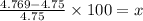
Solving the operations:

`(0.019)/(4.75)*100=x`
`x=0.4`

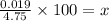
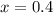
Therefore, the error is +0.4%