Question

At Ms. Elsa's farm, she sold 9 cabbages and 6 carrots for $2100.00, while 5 cabbages and 6 carrots were sold for $1700.00. Assume we use two variables x and y to represent cabbages (x) and carrots (y). Exactly what was the cost of a cabbage?

Answer 1

`x= 100`

`y=200`

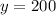
Explanation:

For this question, we will need to use a systems of equations, in which we set up two equations, to solve for some variable.

As stated in the question, the cost of cabbages will be represented as the variable "x" and the cost of carrots will be represented as the variable "y".

If we want to calculate the price of buying "c" amount of cabbages or carrots, we can simply multiply it by the price, which is represented by our variables.

So when the question states 9 cabbages and 6 carrots were bought. we can represent the price of this purchase as the following:
`9x + 6y`

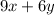
We simply multiply the number of cabbages, by the price "x", to get the total price of buying "9" cabbages, and the same is applied to the carrots.

It's also given in the question that this purchase ended up being $2100.00, so we can set our expression equal to this:
`9x+6y=2100.00`

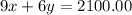
If we do the same with the second set of information given, we can also derive the following equation:
`5x+6y=1700.00`

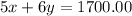
Now we're looking for a "x" and "y" value that will make both equations true, or in other words where these two equations would intersect on a coordinate plane!

We can solve this many ways either by graphing, substitution, or elimination.

I'll show the substitution method.

We start off with these two equations.

`9x+6y=2100.00`

`5x+6y=1700.00`

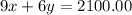
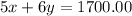
In this case solving for one particular value in a two-variable equation is impossible, since if "x" is some value, well then we can define a "y" value that makes this true, there are infinite solutions.

But in a one-variable equations, we can rearrange the equation, to find a particular solution(s). This is the goal of the substitution method, we want to define "x" or "y" in terms of the other variable, so we can substitute it into the other equation.

So let's solve for "x" in terms of "y" using the second equation:

`5x+6y=1700.00`

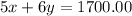
Subtract "6y" from both sides

`5x=1700-6y`

Now divide by "5" to solve for x in terms of "y"

`x=(1700-6y)/(5)`

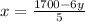
We can distribute the division as such:

`x=(1700)/(5)-(6y)/(5)`

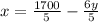
which we can simplify to

`x=340-(6y)/(5)`

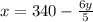
Now we take our other equation:

`9x+6y=2100.00`

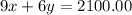
And let's substitute this other definition of "x" we just solved for

`9(340-(6y)/(5)) + 6y=2100`

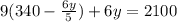
Notice how we now have a one-variable equation, so we can now solve for a particular value!

Distribute the multiplication to get:

`3,060-(54y)/(5)+6y=2100`

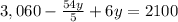
Rewriting our fraction as a decimal we get:

`3060-10.8y+6y=2100`

Combining like terms we get

`3060-4.8y=2100`

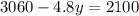
Now subtract 3060 from both sides

`-4.8y=-960`

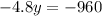
Divide both sides by -4.8

`y=200`

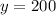
Now let's take either equation and plug this value of "y" in so we can solve for x

In this example I'll use:
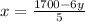`x=(1700-6y)/(5)`, which we derived earlier from one of our initial equations, but you can also use any of the two initial equations.

`x=(1700-6(200))/(5)`

`x=100`

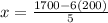
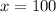
So now we have our two solutions!