Question

Find the probability that a randomly chosen point is the figure lies in the shaded region. Give all answers in fraction and percent forms. help with #6

Answer 1

Answer:

The probability that a randomly chosen point is the figure lies in the shaded region is 36%

Step-by-step explanation:

We need to find the area of the circle, and the square.

To find the area of the square, we need to find the side length. This is done using Pythagorean theorem as follows:

`\begin{gathered} s^2+s^2=8^2 \\ 2s^2=64 \\ s^2=(64)/(2)=32 \\ \\ s=√(32) \end{gathered}`

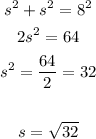
Area of square is now:

`s^2=32`

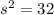
Area of circle is:

`\begin{gathered} A=\pi r^2 \\ =\pi*((8)/(2))^2=16\pi \\ \end{gathered}`

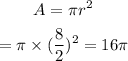
= 50.26548245743669

Area of shaded region is:

50.26548245743669 - 32

= 18.26548245743669

The probability that a randomly chosen point is the figure lies in the shaded region is:

18.26548245743669/50.26548245743669 = 0.3633802276324186

This is approximately 36 percent