Answer and Explanation:
Given the below equation;
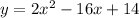
where y = the height/depth of the person's head
x = seconds after leaving the diving platform.
a) We're told that the values of x should go from 0 to 10.
To be able to plot the graph, let's choose different values of x and find the corresponding values of y.
When x = 0;
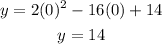
When x = 2;

When x = 6;
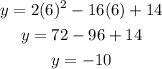
When x = 8;

When x = 10;
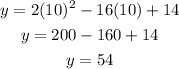
See below the graph of the given equation;
c) We're told from the que