Given:
Mass, m = 0.5 kg
Speed, v = 6 m/s
radius, r = 1.5 m
Let's find the tension in the string.
To find the tension in the string, apply the formula:
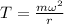
Where;
w is the angular velocity.
To find the angular velocity, apply the formula below:
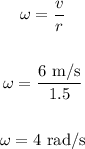
The angular velocity is 4 rad/sec.
Now, find the centripetal acceleration:
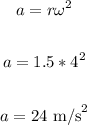
Now, to find the tension, we have:
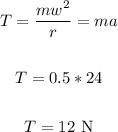
Therefore, the tension in the string is 12 N.
ANSWER:
D. 12N