Question

The sum of three times a first number and twice a second number is 14. If the second number is subtracted from twice the first number, the result is 7. Find the numbers.2, 14, 04, 10, 7

Answer 1

Given:

The sum of three times a first number and twice a second number is 14. If the second number is subtracted from twice the first number, the result is 7.

Required:

Find the numbers.

Step-by-step explanation:

Let the first number be x and the second number be y.

By using the given information the equations become:

`\begin{gathered} 3x+2y=14.....(1) \\ 2x-y=7.......(2) \end{gathered}`

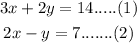
Multiply equation (2) by 2 .

`4x-2y=14......(3)`

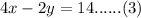
Add equations (1) and (3).

`\begin{gathered} 7x=28 \\ x=4 \end{gathered}`

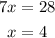
Substitute the value of x in equation (1).

`\begin{gathered} 3(4)+2y=14 \\ 12+2y=14 \\ 2y=2 \\ y=1 \end{gathered}`

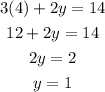
The value of x = 4 and y =1.

Final Answer:

The first option is the correct answer.