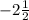Answer:

Explanation:
So, we have
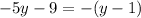
The first thing we need to do is distribute, which makes
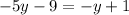
Then, we add 9 to both sides to get rid of the 9 on the left side of the equation, leaving -5y alone
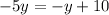
After that, we must remove the y on the right side by adding y to both
sides. Since y is defined as 1, unless said otherwise, we will be left with

Now, this is where it can get a little confusing. At this point, all that's left to do is divide -4y by 4, and 10 by 4, which will give us
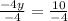

This should be the end of the equation, but we need to simplify it to get our final answer. Since 4 and 10 both share 2 as a common factor, we will use 2 to simplify our fraction, which leaves us with
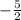
But we still aren't done! Since the numerator is a higher number than the denominator, this is considered an improper fraction, which means we must convert it into a mixed number fraction.
We take the devisor, in this case, 2, and divide it by 5.
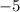 ÷
÷
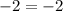
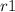
This leaves us with 2, and a remainder of one. Since the denominator stays the same, this will leave us with a final answer of