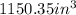Question

Karen of mandible sweets wants to build the worlds largest jawbreaker. To do this she finds that it must have a 13 inch diameter. How much candy will Karen need for one? (volume)

Answer 1

You need to use the formula for calculate the volume of a sphere:

`V=(4)/(3)\pi r^3`

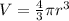
Where "r" is the radius of the sphere.

You know that the diameter of this jawbreaker must be:

`d=13in`

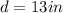
Since the radius is half the diameter:

`\begin{gathered} r=(13in)/(2) \\ \\ r=6.5in \end{gathered}`

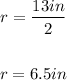
Therefore, substituting this value into the formula and evaluating, you get:

`\begin{gathered} V=((4)/(3))(\pi)(6.5in)^3 \\ \\ V\approx1150.35in^3 \end{gathered}`

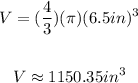
The answer is:

`1150.35in^3`